※ 인공지능 회귀분석 강의 통계와 확률을 바탕으로 정리하였습니다.
2차원 데이터 분석은 크게 2가지 방법으로 볼 수 있다.
1. 수치 지표: 상관계수, 공분산
2. 시각화 그래프: 산점도, 회귀직선 등
공분산
두 변수의 상관관계를 수치화 하기 위한 지표

두 변수의 각각 편차의 곱의 합과 길이 만큼 나눈 것
# 공분산 구하기
np.cov(수학점수, 영어점수, ddof=0)
아래와 같이 매트릭스로 나옴
자기 자신과 자기 자신의 공분산은 분산으로써 결과값이 나옴
array([
[86, 65],
[65,68]
])
하지만, 공분산으로 우리는 상관관계를 파악하기는 쉽지 않다.
왜냐하면 변수의 단위가 변수마다 다르기 때문이다.
ex) (키: cm, 몸무게: kg) 각 두 값은 하나로 공분산을 표현할 때
어느 정도 상관관계가 있는 지 판단하기 어려움
따라서 단위에 의존하지 않는 상관관계를 나타내는 지표가 필요하여 상관계수가 나옴
상관계수(Correlation coefficient)
공분산 값에서 단위에 의존하지 않도록 각 데이터의 단위인 표준편차로 나누어 준 값
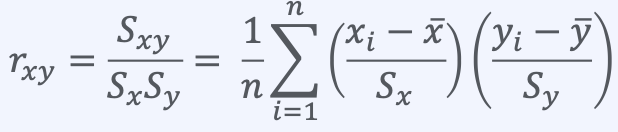
rxy를 상관계수라고 한다.
상관계수는 -1과 1사이의 값을 가진다.
공분산 계산 방법
1. 직접 계산방법
np.cov(수학점수, 영어점수, ddof=0)/(np.std(수학점수)*np.std(영어점수))
2. np.corrcoef() 함수 사용
np.corrcoef(수학점수, 영어점수)
매트릭스로 출력이 되며 자기 자신과 자신의 상관계수는 1이다.
3. DataFrame.corr() 함수
df = DataFrame(수학점수, 영어점수)
df.corr()
데이터프레임으로 상관계수가 출력된다.(넘파이보다 좀더 시각적이다.)
시각화
상관관계가 있더라도 전혀 상관관계가 없는 데이터일 수도 있음
ex) 앤스컴(Anscombe)의 콰르텟 데이터 예시
앤스텀은 데이터셋은 평균,표준편차, 상관관계가 같더라도 전혀 다른 데이터 일 수 있는 사례를 보여줌

따라서 수치 지표를 파악하더라도 시각화는 필수!
대표적 시각화
산점도
matplotlib의 scatter를 통해 대략적인 데이터 분포를 파악
회귀직선
두 데이터 사이의 관계를 잘 나타내는 직선
matplotlib은 회귀직선을 그릴 수 없다 따라서 넘파이로 그려보자
np.polyfit()과 np.ploy1d를 활용하자
히트맵
색의 차이를 통해 표현하는 히스토그램의 2차원 버전
Histd2d 사용
'python' 카테고리의 다른 글
| Polars 라이브러리 문법 정리 [1] (0) | 2023.08.22 |
|---|---|
| 벡터와 벡터 유사성측정 (0) | 2022.05.14 |
| [통계학] 4. 확률 및 통계 (0) | 2022.05.14 |
| [통계학] 1. 산포도 (분산, 표준편차, 사분위) (0) | 2022.05.11 |
| [통계학] 0. 대표값(평균값, 중앙값, 최빈값) (0) | 2022.05.11 |


