optimization이란 머신러닝에서 Y = θ1X + θ0라는 식에서 X라는 input 이 들어왔을 때 Y을 예측하는
Bias, Variance를 고려하여 최적의 θ0, θ1를 구하는 방법론을 말합니다.
1. Derivative 도함수
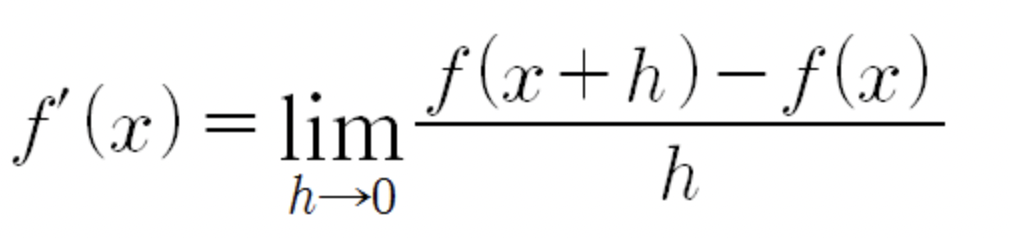
y = f(x)라는 식에서 f(x) 도함수의 해가 0이 되는 해를 구하게 되면 y = f(x)를 만족하는 최적의 기울기를 구할 수 있습니다.
하지만, 이는 함수의 차수가 높아지거나 다변수 함수가 될 경우 계산복잡도가 무한대로 늘어날 수 있다 점
때문에 복잡한 함수인 경우 사용되지 않습니다.(거의 복잡하기 때문에 사용 안해요..)
2. Gradient Descent 경사하강법
머신러닝의 근간이 되는 Optimization 기법으로
Y = θ1X + θ0 라는 식에서 Y-Y^의 값을 최소화하는 θ1,θ0를 구하기 위해서 (Y-Y^) 함수를 미분을 통해서 θ1, θ0를 구하고
이를 기존 θ1, θ0에 업데이트하여 최적의 θ1,θ0를 구하는 방법을 말합니다.
대표적으로 MSE(Mean Square Error)를 예시로 들며 설명해보겠습니다.

MSE는 위와 같은 식으로 정리될 수 있다. m은 예측 값의 개수로 모든 (Y^-Y)**2 값에 대해서 summation을 하고
평균을 내주는 형태입니다.
※ MAE(Mean Absolute Erorr) 같은 경우 square를 취하는 것이 아는 (Y^-Y)의 절대값을 취하는 형태입니다.
※ θ1는 W로, θ0는 bias 로 보통 불립니다.
이러한 MSE(θ1,θ0)를 θ1,θ0에 대한 각각의 편미분을 진행하여 기존 θ1, θ0에 업데이트하는 식으로 최적의 해를 구하게 됩니다.

이를 위해 Learning Rate(step size)라는 가중치를 부여하여 업데이트를 하게 되며 흔히, 𝛼(알파)로 많이 표현이 됩니다.

θ들은 각 θ들의 도함수의 해가 0 되는 방향으로 점차적으로 학습하게 됩니다.
2-1. Learning Rate
step size라고도 불리는 Learning rate는 GD 방식으로 학습을 진행하는 데 있어서 보폭이라고 생각할 수 있습니다.
너무 많은 Learning rate는 오히려 학습되지 못하고 발산하는 형태가 되지만 적절하다면 빠르게 학습이 진행이
될 수 있습니다.

그렇다면 learning rate*error 형태로 업데이트하는 것이 아닌 도함수를 구하고 0이되는
해를 구하면 한번에 최적의 θ1,θ0를 찾을 수 있지 않을까라고 생각할 수 있습니다.
하지만, 위 예시는 간단하게 θ 한개의 대한 그림이라는 점을 유의해야 합니다.

맨 처음 최적화 방법으로 도함수를 소개하면서 얘기했지만 보통 머신러닝에서 학습해야하는 θ는 무수히 많습니다.
위 예시는 θ가 총 2개인 경우를 가정한 cost 그림입니다. 이러한 함수의 도함수가 0인 해를 구하는 것은
계산복잡도가 엄청 높아지기 때문이고 이는 경사하강법을 통해 학습하는 것보다 매우 비효율적입니다.
2-2 Local minima Global minima
Gradient Descent 방식으로 최적의 θ들을 찾기 위해 cost function의 극소(극대) 점을 찾게되는 데
이때 Global minima가 아닌 기울기가 0이 되는 지점을 Local minima라고 합니다.

위 그림처럼 기울기가 0이 되는 cost function의 극소점은 여러개가 있을 수 있으며 가장 Error를 낮추는
극소점 global minima를 찾기 위해서 optimizer라는 기법을 통해 local minima에서 빠져나오도록 합니다.
우리는 cost function의 기울기가 0이 되는 지점이면 모두 최적의 θ를 찾았다고 착각하기가 쉽습니다.
단순히 validation loss 값이 크게 변동이 없다고 하더라도 local minima에 빠진 것은 아닌지 주의를 해야합니다.
헷갈리는 내용
1) 경사상승법
이때 많이 헷갈리게 되는 부분은 경사가 왜 하강하는 방식으로 학습이 되는 것이냐는 것입니다.
이 이유는 흔히 통념적으로 θ-Error로 표현되기 때문입니다.
만약, θ+Error로 표현되었다면 경사상승법(gradient ascent)이 됩니다.
예를 들어 Error를 미분한 식이 x**2이라고 f(X)라고 가정해봅시다. 그렇다면 f(x)의 미분 값이 0이되는
해를 구한다고 하면 극소 값을 구하는 식이 됩니다.
반대로, -(x**2)의 미분 값이 0이 되는 해를 구한다고 하면 극대 값을 구하는 식이 됩니다.
이러한 식이 가능한 이유는 경사상승법, 경사하강법은 최적의 θ1, θ0를 구한다는 점에서 목적이 같기 때문입니다.
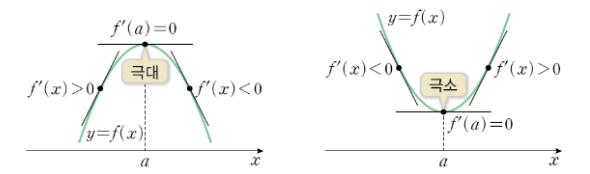
이러한 최적의 θ1, θ0를 구하는 함수를 목적함수(cost function)라고 부릅니다.
2) MSE cost function은 왜 2로 나눌까?

위에서 배웠던 MSE 공식에 의하면 error의 개수만큼 평균을 구하기 위해 1/m 으로 나눈다고 배웠지만
우리는 종종 1/2m 과 같은 수식을 보게 될 것입니다. 이는 편미분의 특성상 연쇄법칙(chain rule)이 작용하게 되면서
square 값이 상수 2로 나오게 되는데 편의를 위해서 이를 2로 나눠주는 것입니다.
전혀 다른 수식이고 결과 값도 다른게 나오는 것 아닌가라고 생각할 수 있겠지만 cost function에 Scaler 값을 곱하는 것은
θ1, θ0 값을 구하는데 영향을 주지 않습니다.
3. Stochastic Gradient Descent 확률적 경사하강법
기존 Gradient Descent는 Full Batch 즉, 모든 θ1, θ0를 업데이트를 할 때 모든 input에 대한 θ1, θ0 값을
구해놓고 한번에 계산하는 방식으로 학습을 진행했습니다.
이때 문제점으로 학습속도가 매우 느리다는 단점과 local minima에 빠지기 쉽다는 점이였습니다.

이러한 점을 보완하기 위해서 stochastic GD(one-batch)가 나왔습니다. 이 방식은 매 input에 대한 θ1, θ0 값을
구하고 이를 바로 update하는 방식입니다. 이는 기존 Full batch 보다는 빠른 속도로 학습이 진행되었지만 성능이
일정하지 않았습니다.
이러한 점을 보완하여 mini-batch라는 방식으로 학습을 진행하게 되었습니다. 아주 보편적으로 진행되는 학습 방식으로
일정한 input 데이터 개수 만큼 θ1, θ0 값을 구하고 이를 update하는 방식입니다.
위 그림처럼 녹색(mini-batch) 선은 다른 학습방식보다 일정하게 그리고 빠르게 학습되는 것을 볼 수 있습니다.
이러한 mini-batch 학습 방법은 GPU 병렬학습을 가능하게 하였습니다.
※ input 데이터가 1000개이고 batch size가 100이라면 10번에 걸쳐서 업데이트가 진행됩니다. 이러한 업데이트를 iteration 이라
부르며 전체 학습 데이터에 대해서 한번씩 학습시킨 횟수를 epoch라고 부릅니다.
--> batch-size: 100, iteration: 10, epoch: 1
만약, 전체 데이터 수가 1010이고 batch size가 100 이여서 수가 딱 맞지 않는다면 1000까지 100 batch-size로 학습을 진행한 후
나머지 10에 대해서 학습을 진행하게 됩니다.
Optimizer
경사하강법을 진행할 시 Local minima 에서 빠져나오면서도 빠르게 학습하는 방식으로
스텝 방향과 스텝사이즈(Learing rate)를 조절하는 방식으로 학습하게 됩니다.

기타 용어
Object function: 학습을 통해 최적화(최대화 or 최소화) 시키려는 함수
ex) Cost Function, Likelihood Function

Loss function : 단일 입력값(x)에 대한 예측값(y^)과 실제 값(y) 사이의 오차를 계산하는 함수
ex)

Cost function : 모든 입력 데이터셋에 대해서 오차를 계산하는 함수, 입력 데이터셋에 대해 계산한 Loss function의 평균 값
ex)

간단히, loss는 단일 학습 데이터의 오차 값, cost는 모든 학습 데이터의 오차 값의 평균, object function은
학습을 통해 최적화(최소화 or 최대화)시키려는 함수를 말합니다.
질문
1. cost function이 무엇인지 loss function, objective function의 개념과 함께 서술해 주세요.
loss function은 모델의 예측값이 실제값을 얼마나 잘 예측했는 지 판단하는 함수로 단일 학습 데이터의 데한 오차 값을
산정할 때 사용됩니다. cost function은 전체 학습 데이터에 대한 오차 값의 평균으로 loss들의 평균으로 정의 될 수 있습니다.
objective function(목적 함수)은 학습을 통해 최적화 시키려는 함수를 말합니다.
2. 아래 수식에서 θ와 𝛼가 각각 무엇인지 서술하세요.

θ0, θ1는 최적화 시키기위해 학습해야되는 함수의 파리미터이며 변화량이라고 볼 수 있다.
이러한 θ들은 편미분을 통해서 각각 기존 θ에 업데이트를 하며 진행될 수록 cost function의 기울기가 0인 지점에
수렴하도록 학습이 진행됩니다. 이렇게 적절하게 학습시키기 위해서 learning rate를 곱한 형태로 업데이트가 진행되는 데
너무 큰 값을 업데이트를 하게될 경우 발산할 수가 있기 때문에 적절한 learning rate 값을 찾아서 학습을 진행하게 됩니다.
3. 미분값으로만 Gradient descent를 진행할 수 없는 이유는?
미분을 통해 기울기가 0인 극소(극대)점을 계산할 수 있지만 머신러닝에서는 θ가 무수히 많아지며 이를 계산할 수는 있지만
계산 복잡도가 무한대가까이 증가할 가능성이 매우 큽니다.
또한, learning rate 없이 미분값만으로 업데이트를 진행하게 될 경우 매우 큰 값을 업데이트
하게되면서 발산할 여지가 매우 커지게 됩니다.
4. [미분적 개념을 참조하자면, 함수는 극점에서의 기울기가 0입니다.] 위 명제가 gradient descent와 어떤 연관이 있는지 서술하세요.
gradient descent는 함수의 극점의 기울기가 0이 되는 부분을 점진적으로 찾아가는 방식으로 학습이 진행됩니다. 왜냐하면 예측값과 실제값의 차이에 미분 함수 값을 업데이트 하는 것은 결국에는 함수의 극점의 기울기가 0이 되는 부분으로 학습되어 지는 것과 매우 비슷하기 때문입니다. 하지만, 무수히 많이 함수의 기울기가 0이 되는 부분이 있을 수 있기 때문에 local minima 빠진 것은 아닌 지 적절한 관찰 과 optimizer를 적용시켜야 합니다.
https://yganalyst.github.io/ml/ML_chap3-2/
https://www.slideshare.net/yongho/ss-79607172\
https://fastcampus.co.kr/data_red_ld
https://ruder.io/optimizing-gradient-descent
An overview of gradient descent optimization algorithms
Gradient descent is the preferred way to optimize neural networks and many other machine learning algorithms but is often used as a black box. This post explores how many of the most popular gradient-based optimization algorithms such as Momentum, Adagrad,
ruder.io
마지막 링크는 다시한번 꼭 보자
'AI' 카테고리의 다른 글
| [차원축소] EVD, SVD, PCA, LDA (0) | 2022.09.06 |
|---|---|
| 차원의 저주(Curse of Dimensionality) (0) | 2022.09.04 |
| XGBoost, LightGBM, Catboost (0) | 2022.08.29 |
| GradientBoosting 하이퍼 파라미터 (0) | 2022.08.27 |
| Gradient Boosting (0) | 2022.08.22 |


